| Lesson 2 | Bitmapped Indexes |
| Objective | Describe B-tree and Bitmapped Indexes. |
Describe B-tree and Bitmapped Indexes
For high cardinality data or data with many possible values, B-tree indexes are most effective. B-tree indexes are most effective for high cardinality data, or data with many possible values. A common problem with traditional B-tree indexes occurs when an indexed column has low cardinality, which means it has too few distinct values to speed query access. For example, an index of a REGION column that has only 4 values (North, South, East, West) does not have enough distinct values to speed access for queries. It is an index column with relatively few distinct values, compared to the number of rows in the table, and is referred to as a low cardinality column. Oracle's answer to the problem of low cardinality is the bitmapped index.
- B-tree Indexes in Oracle:
Traditional B-tree indexes are tree shaped indexes with individual index nodes to contain the high-level symbolic keys and pointer values. The b-tree indexing method refers to a balanced tree whereby tree nodes will split to create new nodes and spawn to create a new tree level as keys are added and deleted.
Problem: You want to create an index. You understand that the default type of index in Oracle is the B-tree, but you do not quite understand how an index is physically implemented. You want to fully comprehend the B-tree index internals so as to make intelligent performance decisions when building database applications.
Solution: An example with a good diagram will help illustrate the mechanics of a B-tree index. Even if you have been working with B-tree indexes for quite some time, a good example may illuminate technical aspects of using an index. To get started, suppose you have a table created as follows:
create table cust (cust_id number, last_name varchar2(30), first_name varchar2(30));
You determine that several SQL queries will frequently use LAST_NAME in the WHERE clause. This prompts you to create an index:
SQL> create index cust_idx1 on cust(last_name);
Note: There is not an explicit CREATE INDEX privilege (although there is a CREATE ANY INDEX privilege). if you can create a table (which requires CREATE TABLE) then you can create indexes on it. You also need space quotas for consuming space in the tablespace the table/index is placed within. Keep in mind that with the deferred segment feature (available only with enterprise edition of database), that it's possible to create a table and index in a tablespace, but not realize the space quotas are required until a record is inserted into the table (and attempts to consume space).
Next several thousand rows are now inserted into the table (not all of the rows are shown here):
Oracle Indexing and Access Paths
Several Thousand rows are inserted
insert into cust values(7, 'ACER','SCOTT'); insert into cust values(5, 'STARK','JIM'); insert into cust values(3, 'GREY','BOB'); insert into cust values(11,'KHAN','BRAD'); ..... insert into cust values(274, 'ACER','SID');
After the rows are inserted, we ensure that the table statistics are up to date so as to provide the query optimizer sufficient information to make good choices on how to retrieve the data:
SQL> exec dbms_stats.gather_table_stats (ownname=>user,tabname=>'CUST',cascade=>true);
oracle strongly recommends that you do not use the ANALYZE statement (with the COMPUTE and ESTIMATE clauses) to collect statistics. oracle does support using the ANALYZE statement for non-statistics gathering uses such as validating objects and listing chained/migrated rows. As rows are inserted into the table, Oracle will allocate extents that consist of physical database blocks. Oracle will also allocate blocks for the index. For each record inserted into the table, Oracle will also create an entry in the index that consists of the ROWID and column value (the value in LAST_NAME in this example). The ROWID for each index entry points to the datafile and block that the table column value is stored in.
- Bitmapped indexes:
We know that the purpose of an index is to provide pointers to the rows in a table that contain a given key value. In a bitmap index, a bitmap for each key value is used instead of a list of ROWIDs. Each bit in the bitmap corresponds to a possible ROWID. If the bit is set, the row with the matching ROWID includes the key value. A mapping function converts the bit position to an actual ROWID, so the bitmap index functions as a regular index although it has a different internal structure. If the number of different key values is small, bitmap indexes are very space-efficient.
Bitmapped index and binary array
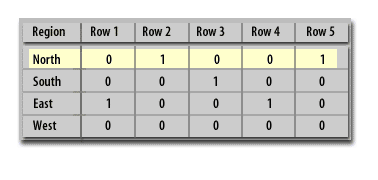
| Region | Row 1 | Row 2 | Row 3 | Row 4 | Row 5 | |--------|-------|-------|-------|-------|-------| | North | 0 | 1 | 0 | 0 | 1 | | South | 0 | 0 | 1 | 0 | 0 | | East | 1 | 0 | 0 | 1 | 0 | | West | 0 | 0 | 0 | 0 | 0 |
This tabular structure aligns with the format seen in the image.
1) In a bitmapped index, a binary array is created with one index row for each table row
Bitmap Indices
Bitmap indexes in Oracle Database can be a powerful tool in SQL Tuning, enabling efficient access to data in certain circumstances. They provide an alternative to traditional B-Tree indexes, which are used in most database systems. A Bitmap index in Oracle uses a bitmap for each key value instead of a list of rowids. Each bit in the bitmap corresponds to a possible rowid: if the bit is set, it means that the row with the corresponding rowid has the key value. When Oracle uses a Bitmap index, it first retrieves the bitmap for the key value it is looking for, then uses a fast algorithm to convert the bitmap into a list of rowids. These rowids can then be used to quickly retrieve the corresponding rows from the table. Bitmap indexes are particularly effective in situations where the indexed column has a low cardinality, meaning it has relatively few distinct values compared to the number of rows in the table. Examples might include a 'gender' column (with possible values 'M' and 'F') or a 'marital status' column (with possible values 'Single', 'Married', 'Divorced', 'Widowed'). The more skewed the data distribution, the more effective the bitmap index.
- Ability to handle complex Boolean Queries:
Another major strength of Bitmap indexes is their ability to handle complex Boolean queries involving multiple conditions (AND, OR, NOT). Oracle can take multiple bitmaps (one for each condition) and perform fast bitmap operations to combine them into a result bitmap. This is much more efficient than having to scan the table multiple times, once for each condition, as you might have to do with a B-Tree index. However, Bitmap indexes do have some drawbacks and limitations. They are less efficient than B-Tree indexes when the data distribution is not skewed and the number of distinct key values is high. Moreover, they can cause contention issues in a multi-user environment where there are concurrent DML (Data Manipulation Language) operations, as multiple sessions may try to update the same bitmap at the same time. To sum up, Bitmap indexes in Oracle Database can greatly improve query performance in specific circumstances, particularly for low-cardinality columns and complex Boolean queries. However, they need to be used with care, taking into account their potential downsides. As always, it is important to thoroughly test any indexing strategy to ensure it delivers the expected benefits.
More on bitmap index
A bitmap index is a special type of index that uses a series of bitstrings to represent the set of ID values that correspond to a given indexed data value. You can define a bitmap index for a field if the table's ID field is defined as a positive integer (see restrictions). Bitmap indices have the following important features:
Subject to the restrictions listed below, bitmap indices operate in the same manner as standard indices. Indexed values are collated and you can index on combinations of multiple fields.
- Bitmaps are highly compressed: bitmap indices can be significantly smaller than standard indices. This reduces disk and cache usage considerably.
- Bitmaps operations are optimized for transaction processing: you can use bitmap indices within tables with no performance penalty as compared with using standard indices.
- Logical operations on bitmaps (counting, AND, and OR) are optimized for high performance.
- The SQL Engine includes a number of special optimizations that can take advantage of bitmap indices.
Subject to the restrictions listed below, bitmap indices operate in the same manner as standard indices. Indexed values are collated and you can index on combinations of multiple fields.